統計学について考えるにつけ、相当哲学的だと思うようになってきた。そして統計学の内部は相当ごちゃごちゃしているので哲学的な視点からの整理が必要なのではないかと思い始めた。もちろん編集中（途中かなり雑）。

全体像 Part 1

大きく分けて統計学はパラメトリックな手法とノンパラメトリックな手法に分かれる。パラメトリックな手法はガウス分布などといった何らかのモデルを想定し、そのパラメータを推定するものであり、ノンパラメトリックな手法はモデルを想定せずに（ビッグ）データからモデルを推定するものだ。従来型の統計学（頻度主義、ベイズ統計（ベイジアンとも言われる）、尤度主義、情報量基準統計学）は基本的にパラメトリックなものであり、これらはデータが大きくない場合やドメイン知識がある場合に使いやすい。一方、ノンパラメトリックな手法はビッグデータ、機械学習などの場合に使われる。

大きくまとめると、基本的に現在の統計学はロナルド・フィッシャーによってその基礎（尤度）が作られ、それに頻度主義確率的解釈および決定理論の要素を加えたのがネイマン・ピアソンらのいわゆる頻度主義統計であり、フィッシャーの考えた尤度は確率理論の公理系を満たしていないから、確率理論の公理系を満たすような形で統計学を再構築しようとしたのがベイズ統計であり、フィッシャーの考案した尤度を推論の中核におこうとするのが尤度主義であり、フィッシャーは尤度に基づいて仮設検定と推定を分けたが、その分け方が適切でないと考えたのが情報量基準統計学（モデル選択）である。このように考えると従来型の統計学は全てフィッシャーの延長線上、もしくはそれに反論する形で進化してきた。これに近年、従来の統計学（および数学）の枠組みを超える因果推論が加わり、フィッシャーの時代には存在しなかったコンピュータやビッグデータが使えるようになったことで、モデルを想定せずにデータから直接モデルを構築するノンパラメトリックな手法（機械学習）が発展し始めた。

全体像 Part 2

基本的には従来型の統計学（フィッシャー、ネイマン、ピアソンらの頻度主義統計）は応用数学のようでいて、実はそうではない。それは数学というよりも道具（ヒューリスティック）と言った方が正確だろう。数学は基本的に公理系から始まり、定理や補題などを証明していく作業だ。だから統計学が応用数学であるならば、統計学も公理系から始まらなければならない。しかし従来型の統計学はそうではない。頻度主義統計は後述するようにフィッシャーが考案した尤度を中核としている。尤度というのは仮説を想定したときのデータの確率、つまり条件的確率のようなものなのだが、実は確率ではない（後述）。フィッシャーは1920年代に現代の統計学の基礎となる尤度などといった手法を作り出したが、それは数学というよりも使用しやすい道具という感じがする。実際に彼の考え出した概念である尤度およびfiducial probability（信頼確率などと呼ばれる）は両者ともに公理系から始まっていない（fiducial probabilityに関しては批判が強く、フィッシャー自身後年諦めた）。これに対していわゆるベイズ統計学と呼ばれるものは確率論の公理系から統計的推論を導き出そうとする。実際に、ベイズ統計学の生みの親の一人であるデニス・リンドリー（およびレオナード・サベージ）は他の数学は全て公理系から始まるのに、（フィッシャー、ネイマン、ピアソンらの）統計学はそうではなかったので、それを公理系によって基礎づけようとした。そして最終的に現在ベイズ統計学と呼ばれるものを生み出した。リンドリー自身1933年に書かれたコルモゴロフの本を翻訳しそれに基づいて授業をしようとしていたのだが、それは当時のイギリスでは新しいことだったということだから、現在とのギャップが色々感じられる（コルモゴロフは確率論を公理化した人物だ）。情報量基準統計学も出自自体は頻度主義であるものの、情報理論に則っており、情報理論は確率論の延長であることから、ベイズとはマッチングが良い。

別に統計学は応用数学でなくても良い。道具として使えるというのならばそれでも良いだろう。実際に頻度主義統計は広く使われている。だが統計学が公理系から始まっていない道具であるということに一抹の違和感は感じるし、そのことによって実際の運用上の問題も出てくる。後述するように、ストッピングルールの問題だったり、サンプルサイズの問題、尤度原理の問題が出てくる。これらの多くはデニス・リンドリーによって提起されたものだ（どこまでオリジナルのアイデアをたどれるのかというのはなかなか難しい問題なのだが）。

頻度主義統計

統計学は基本的には平均とか分散とかいった記述統計と統計的推論に大別される。基本的に統計的推論が出てきたのはチャールズ・ダーウィンの従兄弟であるフランシス・ゴルトンが回帰分析を発見した時あたりからだ。その弟子であるカール・ピアソン、そしてロナルド・フィッシャー、カールの子どものであるエゴン・ピアソンとその研究パートナー、ジャジー・ネイマンあたりが頻度主義統計を作り上げた。もちろん、その他にもスチューデントの名前で知られるウィリアム・ゴセット、エイブラハム・ワルドなども重要人物だが、やはりフィッシャーが20世紀統計学の最重要人物だろう。

フィッシャー

フィッシャーは尤度（likelihood）という概念を考案し、それを統計学の中核に据えた。フィッシャーの統計学については他記事でかいたが、簡単にまとめると、尤度は\[P(O \mid H)\]と記され、仮説（H）を想定した時のデータ（O）の確率（のようなもの）だ（ちなみに後述するように尤度は厳密には確率ではないのだが、P（O｜H）という記述方法は地球学者ハロルド・ジェフリーズが使用し一般的になった条件付き確率の記述方法で、Hという条件の下でOの確率という意味だ）。フィッシャーの統計学は仮説検証（有意検定と呼ばれる）と推定（点推定と呼ばれる）に大別され、両方とも尤度を用いている。仮説検証では帰無仮説と呼ばれる仮説を設定し、その仮説に関して尤度を用いたp値というものを構築して0.05（5%）などあらかじめ決められた水準とp値を比べ、仮説を棄却するかどうか決める。推定では最大尤度と呼ばれる尤度を最大化する点を探す。ゆえにこれは最尤推定と呼ばれる。

ネイマン・ピアソン

ネイマンとピアソンは帰無仮説に加え、対立仮説と呼ばれる仮説と、頻度主義的な考え方である信頼区間と呼ばれるものを持ち込んだ。信頼区間とはコインを投げるといったような実験を何度も繰り返すと、例えば、コインの表の頻度は確率的にどの区間に収束するかというものだ。ネイマンとピアソンの統計学もフィッシャー同様、仮説検証と推定に分けられるが、彼らは信頼区間という概念を持ち込んだゆえに、彼らの推定は点推定ではなく区間推定と呼ばれるものになり、彼らの仮説検証も信頼区間を通して行われる。ネイマンとピアソンにとって仮説検定と推定は信頼区間という概念を通して表裏一体だ。

例えば、次のような仮説検証をしたいとする。

\[H_0: \mu = \mu_0 \quad \text{vs.} \quad H_1: \mu \ne \mu_0\]

そして

\[f(x| \mu)\]

からデータを観察する。

この時、0.05などといった有意水準α（サイズと呼ばれる）を設定し、それに基づいて棄却域を定める。観測されたデータがこの棄却域に入れば、帰無仮説H0を棄却する。つまり母平均μに対して95%信頼区間を構築し（これは、無限に同じ実験を繰り返したときに、95%の確率で真のμを含む区間のこと）、

もしμ0が信頼区間の外にあれば、H0を棄却
もしμ0が信頼区間の中にあれば、H0を棄却しない

ということになる。そしてネイマンとピアソン（特にネイマン）は統計学を意思決定に用いるという決定理論的概念を持ち込んだ。言い換えるならば、ネイマンとピアソンは、検定をリスク最小化の問題として以下のように定式化した。

α：Type Iのエラー（本当は正しいH0を棄却してしまう）

β：Type IIのエラー（本当はH1が正しいのにH0を棄却しない）

検出力（パワーと呼ばれる）：1−β（効果があるときにそれを検出できる確率）

そして彼らは尤度比検定

\[\Lambda(x) = \frac{L(\theta_1 \mid x)}{L(\theta_0 \mid x)} = \frac{P(x \mid \theta_1)}{P(x \mid \theta_0)}\]がType Iのエラーα（これは有意水準に等しい）を固定した上で検出力を最大化させる（Uniformly Most Powerful, UMP）ということを示した（ネイマン・ピアソンの補題）。

ちなみにネイマン・ピアソンの補題はその帰結としてフィッシャーの統計学が欠いていた、①棄却域（critical region）を恣意性なく決定させること、および②十分統計量（sufficient statistic）を可能にした。ネイマン・ピアソンの統計学はネイマン・ピアソンの補題によって棄却域を一義的に決定する。①フィッシャーの統計学では棄却域は「起こる確率が非常に少ない」という形で定義されたが、それだったら（論理的に言うならば）正規分布の端っこの方の領域でなくても、正規分布の真ん中の方のすごく狭い領域を棄却域に選んでも良いはずだ。ネイマン・ピアソンの統計学はこのような恣意性をネイマン・ピアソンの補題によって排除した。また、②フィッシャーの統計学では原理上統計量は複数構築することができ、その構築の仕方に棄却するかどうかの判断が依存するという問題があったが、ネイマン・ピアソンの統計学はこのような恣意性をもネイマン・ピアソンの補題によって排除した。

ネイマンは信頼区間を手続きであると捉えた。すなわち信頼区間とは何度もコインを投げるといったような同じ実験をなん度も繰り返す中で、95%といったような一定の頻度で真のパラメータ値を含むような区間を構築する手続きだ。ゆえにネイマン＝ピアソン流の推定では、フィッシャーのように最尤推定により尤度を最大化する一点を推定するのではなく、推定=信頼区間ということになり長期的に見たときに（理想的には極限値で）既知の確率で真の値を捕捉する区間をつくることに等しい。

フィッシャーとネイマン・ピアソンの違い

フィッシャーにとって仮説検証と推定は純粋に推論問題（尤度というのは証拠がどれだけ仮説を支持しているのかという基準だ）だったが、ネイマンにとってはそれらは行動（意思決定）のための手段だった。だからこそ彼らは対立仮説を持ち込んだ。　そうすることで統計学を帰無仮説と呼ばれるH0を棄却するのかしないのかというyes/noの二択の意思決定にしようとした。ここがフィッシャーとネイマン、ピアソンの考え方の大きな哲学的差異だ。ネイマン、ピアソンとフィッシャーは皆ユニバーシティ・カレッジ・ロンドンに所属していたが、このような統計学に対する哲学の違いから強いライバル関係にあり、往往にして（フィッシャーの側から）感情的な議論に発展した。当時ユニバーシティ・カレッジ・ロンドンは世界に唯一の統計学の学部を有していたが、ネイマン、ピアソンとフィッシャーの感情的問題などもあり、統計学部はカールの子、エゴン・ピアソンが引き継ぎ、フィッシャーは優生学部を引き継いだ（チャールズ・ダーウィンの思想を人間に応用する優生学もフランシス・ゴルトンが考えたものだ）。

この問題に関しては基本的に私はフィッシャーが正しいのだと思う。意思決定の道具としての統計学はあっても良いが、そして次に述べるように工場におけるクオリティーコントロールなどといった非常に有用な場面があるが、それは派生的なものであり、基本的に統計学は推論であると思う。のちに述べるベイズ統計学も統計を推論であると考えている。そしてこの統計学にどこまでの要素を含めるのかといった問題が、これものちに述べるように、頻度主義（特にネイマン・ピアソン）、ベイズ統計、尤度主義などといった異なる考え方を引き起こす一因となる。決定理論＋推論というのが頻度主義（特にネイマン・ピアソン）であり、推論＋前提というのがベイズ統計、そして純粋に証拠（データ）からの推論のみ（だと勝手に思い込んでいるのが）尤度主義だと思う。

その後

しかし結局議論に決着がつく前に、ネイマンはアメリカのUCバークレー校に移籍し、ネイマンらの統計学を引き継いだコロンビア大学のエイブラハム・ワルドがエラーレート（間違う確率）を損失関数として形式化し、統計学を（意思）決定理論として形式化した。このような長い実験（頻度主義）を行う中でどのくらいのエラーが出るのか（損失関数）、そしてそうした場合どのように行動するのか（決定理論）という統計学は当時、工場で大量生産を行なっていたアメリカにおいてクオリティー・コントロールの必要性があったことから大きく広がった。

しかし同時にフィッシャーの統計学の考え方とネイマンらの統計学の考え方の違いに関しては結局着地点を見ることなく、その間に痺れを切らした社会科学者たちが教科書を書き始め、フィッシャーとネイマンらの統計学は変な形で組み合わされ使われるようになった。そして社会科学や心理学がソフトサイエンスから自然科学のようなハードサイエンスになろうとする過程で、p値および棄却水準である0.05などといったものが、「客観的」な数字であるような扱い方をされるようになってしまった。これが現在まで続くpハッキングなどと呼ばれる問題を引き起こすことになった。

尤度

フィッシャー、ネイマン、ピアソンの統計学はすべてフィッシャーが考案した尤度に基づいている。尤度はデータ（O）を固定し、仮説（H）を想定した時にそのデータが得られる確率のようなものなのだが、正確には尤度は確率ではない。数学は基本的に公理系からの演繹推論であり、確率理論も数学である以上確率の公理を満たさなければならないのだが、尤度は確率の公理を満たさない。

\[\textbf{Axiom 1(Non-negativity):} \quad \text{For any A, }\quad P(A) \geq 0 \quad \ \]

\[\textbf{Axiom 2(Normalization):} \quad P(\Omega) = 1.\]

\[\textbf{Axiom 3 (Additivity):} \quad \text{If } A_1, A_2, \dots \text{are mutually exclusive, } P\left( \bigcup_{i=1}^{\infty} A_i \right) = \sum_{i=1}^{\infty} P(A_i).\]

確率の公理の1と2は確率は0以上であり、全て足し合わせると1になるということを言っているのだが（つまり確率は0%から100%の間の数値しかとらない）、尤度は定理2である正規化を満たしておらず、1（100%）以上になってしまうことがある。例えば、正規分布

\[X \sim \mathcal{N}(\mu, \sigma^2)\]

を見てみると、確率密度関数は
\[f(x \mid \mu, \sigma)
= \frac{1}{\sqrt{2\pi\sigma^2}}
\exp\left[-\frac{(x – \mu)^2}{2\sigma^2}\right]\]

となり、σ = 0.1として最大密度をみると

x = μなので\[(x – \mu)^2=0\]

であり、

\[\exp(0)=1\]

で
\[f(\mu \mid \mu, 0.1)
= \frac{1}{\sqrt{2\pi(0.1)^2}}
\approx 3.989 > 1\]

となる。

つまり厳密にいうと、尤度を用いた統計学は数学ではなく、ヒューリスティックな道具であるということになる。このあたりはフィッシャーがどのように統計学を作ったかを読んだらわかるだろう。もちろん統計的推論自体を作ったのがフィッシャーであり、当時はコンピュータなど存在せず、大量演算ができなかったことなどを考え合わせるとヒューリスティックな道具としての統計学は大変有用なものだっただろう。

そしてフィッシャーの統計学（尤度）が公理に基づいていないというのは、フィッシャーが一方的に悪いわけではない。上記でデニス・リンドリーは1933年に書かれたコルモゴロフの本を翻訳しそれに基づいて授業をしようとしていたと言った（そしてリンドリーは統計学自体を公理化しようとした。この結果がベイズ統計学だ）が、フィッシャーの統計学は1920年代にロサムステッド研究所で始まった。つまりフィッシャーが統計学を構築した際には確率は公理化されていなかったということだ。確率の公理という概念自体がなかったといって良い。ちなみに1933年にドイツ語で書かれたコルモゴロフの本が英語に翻訳されたのは1950年のようだ。

ベイズ統計

しかし20世紀中盤あたりから、フィッシャーらがいなくなった後、統計学の聖地であり、頻度主義統計学の聖地でもあるユニバーシティ・カレッジ・ロンドンで研究をしていたデニス・リンドリーらの統計学者らは厳密にいうと数学でない、つまり公理系から始まらない道具としての統計学に疑問を抱き始めた（リンドリーの場合はフィッシャーの唯我独尊的な態度が嫌いだったということもある）。ベイズ統計の創始者らはブルーノ・デ・フィネッティ、レナード・サヴェッジ、デニス・リンドリー、ハロルド・ジェフリーズ、I.J.グッドらだろう（因みにサヴェッジは高名な経済学者ミルトン・フリードマンの弟子であり、ジェフリーズは相対性理論の最初の実験を行ったアーサー・エディントンの弟子であり、グッドはコンピュータの生みの親アラン・チューリングのアシスタントだった）。

彼らは確率理論の公理系から導かれるベイズの定理\[P(H \mid O) = \frac{P(H) \cdot P(O \mid H)}{P(O)}\]を用いて統計学を再構築しようとした（定理とは公理から演繹的に導かれるものだ）。ここでも尤度は出てくるが分母である正規化定数が存在するので全ての確率を足し合わせるとこれは1になる。ベイズ統計の観点からは統計学は意思決定の道具ではなく、信念（自分が何を信じるか）の程度であると考え、事前確率\[P(H)\]、つまり自分がそれまで何を信じていたのかを、新しいデータを見た際に、尤度によってアップデートするという考え方をする。

頻度主義統計は何度もコインを投げるといったような、究極的には極限値（公正なコインを無限に投げると、表の頻度は0.5=50%に収束するという考え方）を得られる「客観的」な確率概念に依拠しているが、ベイズ統計は確率は自分が何を信じるかという自分の主観だと考えるし（正確にいうと頻度主義統計でも主観確率は使えるし、ベイズ統計でも頻度主義的確率概念は使える。厳密には確率の解釈と統計手法とは次元が異なる話だ）、統計計算に「客観的」でない主観確率を持ち込んだ。「客観的」科学を行う際に、主観を持ち込むというのはどういったことなのだろう。これは大きな議論を呼んだ。

フィッシャーは統計的推論を仮説検証と推定に分けた。ネイマン・ピアソンもそれに従った。ベイズにおいてそれに対応するのが、推論と最適化だ。フィッシャーは両方を尤度を使って行った（有意検定と点推定）。ネイマン・ピアソンは両者を信頼区間を使い行った（尤度比検定と区間推定）。後述するようにベイズ統計では仮説検証はベイズファクターなどを用いる（ここではMCMCがサンプリング手法として使われる）。推定には勾配法などを用いる。フィッシャーによる推定は尤度を解析的に最大化させる最尤法による点推定であり、基本的には最適化だ。しかしパラメータが多い場合（ディメンションが高い場合）、解析的な点推定（最適化）は難しくなる。尤度を最大化させる点推定は基本的には（第一）微分＝0の場所を探すことだが（第一微分は曲線の傾きを示し、曲線の傾きが0の点は少なくともローカルな極小か極大だ）、イメージ的に考えると、カーブが複雑になると微分＝0の場所が複数存在し、ローカルな極小か極大に捕まってしまい、グローバルな極小や極大にたどり着けない可能性が出てくる。ヘッセ行列（第二微分を集めたもの）を使いConcaveやConvexであることがわかるとローカルな極小、極大はグローバルな極小、極大であることが保証されるので、ニュートン法や勾配法を使って（ステップサイズというハイパーパラメータを調整すると）基本的にはグローバルな極小、極大にたどり着く。しかしそうでない場合など、Adamなどモメンタムなどの物理学にインスパイアされた方法を使い最適化を行う（MCMCにモメンタムなどの考え方を足したものがハミルトニアンMCであり、熱という考え方を加えたものが焼きなまし法であり、勾配法にもメンタムなどを足したものがAdam、熱という概念を加えたものがやはり焼きなまし法だ。焼きなまし法はローカルか極小から逃れる手段でサンプリング（推論、仮説検証）、つまりMCMCでも推定（最適化）でも使われる）。

尤度原理

ベイズ統計は尤度原理を満たす。尤度原理（likelihood principle）をどのように理解するのかということが頻度主義統計とベイズ統計そしてもう一つのパラダイムである尤度主義（likelihoodism）という三つの統計学のパラダイムの哲学的差異に関わってくる（後にモデル選択、因果推論という二つのパラダイムについても語る）。尤度原理とは尤度にデータに関する全ての情報が入っているという考え方だ。ベイズ統計における事後確率は事前確率および仮説を想定した時のデータの確率（のようなもの）である尤度で決まるので、データに関する全ての情報は尤度の中に入っているということになる。一方、頻度主義統計は尤度原理を満たしていない。別のところで話したが、頻度主義統計はいつ実験を止めるのか、という実験デザインやストッピング・ルールに影響されるので、尤度が全く同じでも、結果は異なることになる。

統計学者アラン・バーンバウムはかつて、尤度原理を受け入れるのであれば、ベイズ統計あるいは尤度主義といった尤度に基づく方法を受け入れなければならず、実験デザインやストッピング・ルールに依存するp値や信頼区間のような頻度論的手法は否定されるべきであると主張した。彼の主張は基本的に以下のようだ。

十分性原理（Sufficiency Principle, SP）：データに含まれるすべての情報が十分統計量によって要約されるのであれば、推論はその統計量のみに依拠すべきである。

条件付き原理（Conditionality Principle, CP）：複数の実験の中から（例えばコイン投げによって）ランダムに1つの実験が選ばれた場合、推論は実際に行われた実験のみに基づくべきであり、行われなかった他の実験に基づいてはならない。

尤度原理（Likelihood Principle, LP）：仮説に関するすべての証拠は尤度に含まれている。すなわち、同じ尤度を持つ異なる実験結果は、同じ推論を導くべきである。

そして彼は以下のように主張した。

SP + CP ⇒ LP

つまりもし十分性原理と条件付き原理の両方を受け入れるのであれば、必然的に尤度原理も受け入れなければならないということになる。

尤度原理と頻度主義統計

明確に頻度主義統計は尤度原理と対立する。なぜならp値や信頼区間といった頻度論的な手法は、サンプリング分布や観測されなかったデータ（反事実）に依存しており、それは明確に尤度原理に反することになる。

この場合どうすれば良いのか。最も簡単な方法は頻度主義統計をダメだと切って捨てることだ。私自身はそこまで極端ではないが、心情的にはこれが正しいと思っている（正直、頻度主義にはあまり未来がないように思える）。p値や信頼区間、有意検定などは公理系から一貫性を持って導かれた数学ではないので、基本的にはダメなのだが、まあ道具ではあるので、使える範囲でその限界を意識しながらであれば有用な道具だと思う。

頻度主義統計とベイズ統計の関係性は、例えるならば、ニュートン力学と量子力学のような関係性だと思う。頻度主義は長期的な頻度や事前に決まったサンプリング計画、実験計画に基づき、観測者に依存しない客観的な外からの視点であり、独立同分布の試行、既知のサンプリング計画、仮想的な繰り返しにおける誤差制御などを前提とする理想化された仮定のもとで行われるが、ニュートン力学が微小スケールや高速で破綻するように、頻度論も高次元で複雑なモデルでは限界を露呈する。

一方ベイズ統計の観点からは、推論は観測データと事前知識（事前確率）に依存し、客観的な神の視点は存在しない。つまり量子力学が観測者に依存するように事前確率という実験者の主観が入り込むことになる。一見すると、主観が科学に入るというのはショッキングであるが、それが推論の自然な状態である。ベイズ統計の観点からは、どのような推論であれ推論は様々な前提、仮定に基づいて行われる。前提、仮定の存在しない推論など存在し得ない。そしてベイズ統計はその前提、仮定を事前確率という形で隠さずに提示しているわけだから、その方が余程正直なのではないだろうか。そしてもし前提、仮定に誤りがあるのならば、それを修復することも簡単だ。しかし物理学者が今でもロケットや橋梁の設計にニュートン力学を使うように、限界さえ理解していれば、頻度論的手法を使うことには何も問題はない。これが私の基本的な考えだ。

ベイズ統計の方がそのほかの手法よりも有用であるという理由はさらにある。頻度主義統計であるネイマン・ピアソンの仮説検証では尤度比である以下を求め、それをkと比べて棄却するかどうかを決定する。ここでkはType Iのエラーをコントロールするのに選ばれた定数。

\[\Lambda(x) = \frac{L(H_1 \mid x)}{L(H_0 \mid x)} = \frac{P(x \mid H_1)}{P(x \mid H_0)}\]

\[\text{棄却 } H_0 \text{ if } \Lambda(x) \leq k\]

すでに述べたようにネイマン・ピアソンはType Iエラーの確率を棄却水準αに保つすべての検定の中で、H1（対立仮説）が正しいときにH0（帰無仮説）を最も高い確率で棄却できる検定は尤度比をある閾値と比較して判断する検定が最強（uniformly most powerful, UMP）の検定である、ということを示した。

しかしこれは頻度主義である以上、当然ながら実験計画、サンプリング計画、ストッピング・ルールなどに影響され、尤度原理を満たさない。

頻度主義統計とサンプルサイズの問題

さらに頻度主義統計にはサンプルサイズを大きくすると、帰無仮説を自由に棄却できるようになるという問題もある。帰無仮説を以下のように設定する。

\[H_0: \theta = 0\]

今、以下のようなサンプルを得たとする。

\[x \sim \mathcal{N}(\theta, \sigma^2 / n)\]

この時スタンダードエラーは以下のようになる。

\[\text{SE} = \frac{\sigma}{\sqrt{n}}\]

Z統計量は以下のようになる。

\[z = \frac{x – 0}{\sigma / \sqrt{n}} = x \cdot \frac{\sqrt{n}}{\sigma}\]

今、サンプルサイズnを増やしていくと、分母はどんどん小さくなり、z統計量はどんどん大きくなる。zが大きいということはp値は小さいということであり、0.05などといった任意の棄却基準で棄却できることになり、結果を自由に「有意」とすることができる。もちろんストッピングルールの問題と並び、これはとても問題だ。世間的なイメージだと事前確率を使用するベイズ統計は頻度主義に比べて恣意性が高いと思われているかもしれないが、推論はすべからく前提なしではできないということを考えるならば、事前確率はそれらを詳らかにしたものであり、なんら問題はないと思う。逆に頻度主義の方に恣意性がシステマティックに存在するように思う。

尤度原理とベイズ統計

一方、ベイズ統計では同じような状況でベイズファクターと呼ばれるものを使う（正規化定数は打ち消しあい消える）。

\[\frac{P(H_1 \mid O)}{P(H_0 \mid O)} = \frac{ \frac{P(H_1) P(O \mid H_1)}{P(O)} }{ \frac{P(H_0) P(O \mid H_0)}{P(O)} } =\frac{P(H_1) P(O \mid H_1)}{P(H_0) P(O \mid H_0)}\]

今、ストッピングルールを

\[\binom{n}{k} \cdot p^k \cdot q^{n – k}\]

として、H1をP=0.5、H0をP=0.6とすると（そして簡潔のために事前確率は全く同じだと想定したので事前確率も打ち消しあって消える）、

​​\[\frac{P(O \mid H_1)}{P(O \mid H_0)} = \frac{nCk \cdot p^k \cdot q^{n – k}}{nCk \cdot p’^k \cdot q’^{n – k}} = \frac{20C6 \cdot (0.5)^6 \cdot (1 – 0.5)^{20 – 6}}{20C6 \cdot (0.6)^6 \cdot (1 – 0.6)^{20 – 6}} = \frac{(0.5)^6 \cdot (1 – 0.5)^{14}}{(0.6)^6 \cdot (1 – 0.6)^{14}}\]

となりストッピング・ルールは打ち消しあい消える。つまりベイズは尤度原理を体現している。

またベイズ統計では仮説検証は事後確率を計算（推論）することによって算出されるが、ほとんどの場合、パラメータが多すぎたり（ディメンションが高い）、キャッチオール仮説（正規化定数を計算するためには可能なすべての仮説をリストアップしなければならないが、そんなことは事実上無理であるという問題）の問題が出てきたりして、正規化定数を計算することができないため、事後確率は解析的に計算することができない（ここで解析的というのは積分であり、ディメンションが高すぎると積分できない）。そのためマルコフ連鎖モンテカルロ（MCMC）などを用いる。MCMCはシミュレーションであるが、観察されたデータ、尤度、事前確率のみに依拠しており、尤度原理に反しない。ブートストラップなどのリサンプリング手法は観察していないデータを生成するため尤度原理を破ることになる（ブートストラップは既存のデータからリサンプリングすることで仮想のデータを作ることができるが、これは実際には観察されていないデータである）。

ベイズ統計とサンプルサイズの問題

ベイズはベイズファクターを使って計算するので、帰無仮説の時には尤度が非常にシャープになるが、対立仮説の場合、事前確率は確率質量をパラメータ空間に広く見積もってしまう。だからベイズは帰無仮説を選ぶことになる。つまり

\[\text{BF}_{01} = \frac{P(\text{O} \mid H_0)}{P(\text{O} \mid H_1)}\]

の時に、

\[H_0: \theta = 0\]

\[H_1: \theta \neq 0\]

を考えると、帰無仮説H0では狭いパラメータ空間に確率が集中しているが、対立仮説であるH1ではそうはならない。ゆえにこの場合ベイズだと帰無仮説を選ぶことになり、頻度主義とまるで逆の結果となる。これはベイズはオッカムの剃刀を体現しているからだ。ベイズファクターを計算する際には、事後確率は周辺尤度を事前確率全体で積分するので事前確率が広い範囲に確率を分散させることになる。広いパラメータ空間にかかる仮説は当然複雑であり、オッカムファクターはそれに対して罰則を与えることになる。

尤度原理と尤度主義

しかし尤度原理を正しい原理だとしながらも、事前確率を嫌う一派があり、それは尤度主義と呼ばれるパラダイムだ。

\[\frac{L(H_1 \mid O)}{L(H_0 \mid O)} = \frac{P(O \mid H_1)}{P(O \mid H_0)}\]

尤度主義の考え方は哲学者イアン・ハッキング、統計学者リチャード・ロイヤル、そして哲学者エリオット・ソーバーらあたりからきているのだが（ハッキングは後に考えを変えた）、基本的には主観などというものを取り除いて、純粋に「客観的」証拠（データ）だけを考えようというものだ。しかし推論には必ず前提、仮定が必要なことを考えると、一体何がしたいのかがわからない。

因みに尤度主義では通常、Type I、Type IIなどといった頻度主義的エラーレートを扱わない。しかロイヤルは次のように考えた。「H0 が真であるにもかかわらず、H1を強く支持するような証拠が出る確率」、すなわち誤導確率は以下のように考えられる。

\[P\left( \frac{L(H_1)}{L(H_2)} \geq k \,\middle|\, H_2 \text{ が真} \right) \leq \frac{1}{k}\]

ここで「強い証拠」とは、尤度比が閾値を超えることを意味する。

\[\frac{L(H_1)}{L(H_2)} \geq k\]

このとき、「H0が真であるにもかかわらず H1に有利な強い証拠が出る確率」は1/k に抑えられることになる。これがロイヤルの主張だったのだが、この計算は観測されなかった可能性のあるデータ（反事実的データ）に基づいて確率を計算しているため彼自身の主張する尤度原理に反している。

複合仮説の問題

ここまでで頻度主義は尤度原理を満たさないということはわかったが、さらに仮説が単純仮説ではなく複合仮説になった場合、頻度主義と尤度主義は対応できないが（全く対応できないというわけではなく、ある程度はできる）、ベイズ統計は問題なく対応することができる。ここでいう単純仮説とはH1=0.5のように仮説が完全に特定されており、その中に変動するパラメータを持たない仮説のことで、複合仮説とはH0<0.5といったように仮説が完全に特定されておらず、その中に変動するパラメータを持つ仮説のことだ。複合仮説の場合、ネイマン・ピアソンの検定は最尤度を取り計算するのだが、そうすると検定はもはやUMPではなくなることがわかっている。ネイマンとピアソンが尤度比検定はUMPであると示したネイマン・ピアソンの補題は単純仮説飲みに当てはまり、複合仮説には当てはまらない。

同様に尤度主義でもその場合、最尤度を取り計算（比較）するのだが、この場合、解釈が難しくなるし、仮説的データを用いることになるので、推論は実際に行われた実験のみに基づくべきであり、行われなかった他の実験に基づいてはならないという尤度主義が尊重する尤度原理を破ってしまうことになる。

一方、ベイズは周辺尤度を使って複合仮説を自然に扱うことができる（パラメータはθと表記）。ちなみにこれがベイズファクターの構成要素であり、これを近似したものがBICである。BICはベイズ統計学の視点からのモデル選択の基準であり、ベイズファクターもモデル選択の基準であることから、基本的にこれらは同じものであるということができる。

\[P(O \mid H_0) = \int_{\Theta_0} P(O \mid \theta) \, P(\theta \mid H_0) \, d\theta\]

つまり仮説が含むパラメータ空間全体にわたって、事前分布によって重み付けを行う。また、複合仮説間の比較をベイズファクターを用いて行うことができる。

\[\text{BF}_{10} = \frac{P(O \mid H_1)}{P(O \mid H_0)}\]

複合仮説の場合であっても、ベイズ統計では事前分布を用いてパラメータ空間全体にわたって積分を行うので、観測されなかったデータやサンプリング計画には依存しない。つまりベイズ統計は複合仮説の場合でも尤度原理を完全に満たすことになる。

尤度原理と因果推論

基本的に私は尤度原理を正しいものだと考えており、尤度原理を満たさない頻度主義や尤度主義よりもベイズ統計が正しいと思う。尤度原理に一つ例外があるとするとそれはdo演算（do calculus）を用いる因果推論だろう（ドナルド・ルービンは異なる方法論を用いているようだ）。頻度主義統計、ベイズ統計、尤度主義など伝統的な統計学は因果推論には当てはまらず、因果推論は統計への切り口が全く異なる。因果推論はそのほかの統計手法に対してorthogonalな(直行する)感じだ。尤度原理は因果推論と何らかの形で組み合わされなければならないだろう。ただ、因果推論はベイズ統計と親和性を持つとは考えている（実際、因果推論のリーダーであるジュディア・パールはそれ以前にはベイジアン・ネットワークなどの構築を行った）。おそらく次のようになるのではないか。従来型統計学の場合、相関関係に基づいた帰納推論であるので、基本的には尤度原理は満たされなければならない。ゆえにベイズ主義が「一番」正しいということになるだろう。

しかしベイズ統計学における事前確率（や機械学習におけるハイパーパラメータチューニングや特徴量エンジニアリング）のように、推論（モデリング）にはエクストラ・エンピリカルな要素が入ってくる。尤度原理とは尤度にデータに関する全ての情報が入っているという考え方だが、相関関係に基づいた帰納推論を超えた因果推論は反事実分析などデータ以外、つまりエクストラ・エンピリカルな思考を必要とする。そして私は実証主義者ではなく、プラグマティズムが正しいと思っているので、推論（モデリング）は結局アブダクションだと思う。だからこそ従来型の（パラメトリックな）統計学ではベイズ主義が「一番」正しいということになるのだと思う。それ以外も「一番」ではないものの、そして尤度原理を満たさないながらも、ある程度は使えるということになる。

従来型の統計学はゴルトン、カール・ピアソン、フィッシャーらから始まっているが、相関関係ということを発見したのはゴルトンであり、その弟子であったピアソンが統計学を相関関係の学問として定義した。ゴルトンが回帰分析を発見した際に、彼は親の身長から子どもの身長を割り出したが、実は子どもの身長からも親の身長が割り出せることを発見した。つまりそれは因果関係でなく相関関係であるということになる。実際に相関関係という言葉自体を作ったのもゴルトンだ。そしてカール・ピアソンは若き日に実証主義者であり、実証主義は形而上学（メタフィジックス）を排除し、観察可能（エンピリカル）なもの、つまり実証的なデータのみから理論（モデル）を構築しようとする。だからこそピアソンはゴルトンの考えを推し進め、統計学から因果関係を排除し、統計学を相関関係の学問として定義した。しかし意味のない相関という意味で擬似相関という言葉を作ったのもピアソンだ。それが何を意味するか。意味のない相関は当然、意味のある相関との対比の中で存在する。つまりここにはピアソンの思考の矛盾が露呈している。意味のある相関というのは因果関係でしかあり得ない。つまり統計学（モデリング）には実証主義者が形而上学（メタフィジックス）として排除しようとした反事実、因果関係などといったエクストラ・エンピリカルな要素が必要であるということになる。

情報量基準統計学（モデル選択）

さらにベイズ統計は、頻度主義や尤度主義と異なり、確率理論の公理系から一貫して導かれた「数学」であるため、同じく確率理論の公理系から一貫して導かれた情報理論とも整合性が高い（実際、最適化された情報処理を想定すると、情報理論からベイズの定理を導き出すことができる。言い換えるならば、情報のロスがない情報伝達は即ちベイズ推論であるということになる）。ここで頻度主義から現れたが情報理論の枠組みを採用している赤池情報量基準（AIC）などのモデル選択理論というのももう一つの統計学の系譜だ。この系譜は頻度主義統計とベイズ統計を繋ぐブリッジのようなものだと思う。

フィッシャーの統計学は尤度に基づき、仮説検証（有意検定と呼ばれる）と推定（点推定と呼ばれる）に大別されるが、赤池弘次はこれに違和感を抱いた。なぜなら回帰分析、時系列分析などでは仮説検証と推定という区分自体が意味をなさない。それは両方である。さらに重要なことに、ベイズ統計にしても頻度主義や尤度主義にしても、今まで見てきた中で全てが前提しているのは仮説がすでに存在するという点だ。当然ながらベイズ統計にしても頻度主義や尤度主義にしても全て尤度を用いており、尤度は仮説がなければ構築できない。つまりフィッシャー以降の統計学の考え方は全て科学哲学において使われる「仮説の発見過程」と「仮説の検証過程」という考え方を前提としており、それらが問題としていたのは「仮説の検証過程」のみだった。しかし回帰分析、時系列分析などは「仮説の発見過程」と「仮説の検証過程」という区別すらも意味をなさない。

赤池はチャールズ・サンダース・パースのアブダクションという仮説の発見の論理に影響を受け、情報理論に基づき、AICを構築した。AICは最初仮説を持っていなくてもパターンの予測を可能にする（これがAICがBICと大きく異なる点だ）。そしてこれは統計的推論が始まったフランシス・ゴルトンの回帰分析に一定の決着をつけるもの（データに対してどのような回帰線を選ぶか）であるといっていいだろう。そしてAICは尤度主義が対応できないバイアス・バリアンス・トレードオフに解決策を与えるものだ。尤度主義者であるソーバーはAICを尤度主義のパラダイムに取り込もうとしているが、あまり成功しているとは言えない。

ベイズ統計学もまたバイアス・バリアンス・トレードオフを体現している。これはオッカム・ファクターと呼ばれるものでこれを近似したものがベイジアン情報量基準（BIC）であり、これはAICに影響を受けて作られた。やはりAICはベイズと頻度主義を繋ぐものなのではないか。

認識論的には

認識論的に見ても各パラダイムは異なる考え方を持つ。フィッシャーは統計学を推論と考えていたようだし、また統計学は情報を減らすことの研究だ、という旨の発言もしている。これは情報理論の観点からはモデリングは情報の圧縮であるという考え方と一致する。ネイマン・ピアソンは統計学を意思決定の指針、つまり決定理論だと考えた。ワルドはその方向性を推し進めた。ベイズ統計は統計学を信念の度合い、アップデートだと考える。尤度主義はおそらく統計学を証拠（エビデンス、データ）の客観的な比較だと考えるのだろう。因果推論はおそらくかなり独自で、そのほかの統計が相関関係による世界の「記述」であるのに対して、因果関係を入れた「説明」を行おうとする。AICなど情報量基準統計学はモデルが真実かどうかではなく、予測を中核に据えていると考えられる。

ノンパラメトリックな手法

上記はすべていわゆるパラメトリックな手法と呼ばれる、何らかのモデルを想定（仮定）して、その上でそのモデルが持つパラメータを最適化する方法だ。しかしパラメトリックな手法には想定したモデルが良くないと統計推論自体がうまくいかないという問題がある。パラメトリックな手法はデータが小さく、ドメイン知識がある場合、有効だ。しかしそうでない場合、そしてデータが大きい場合（ビッグデータ）、コンピュータの性能の上昇もあり、モデルを想定せずにデータからモデルを生成させるというノンパラメトリックな手法が有効になる（場合もある）。パラメトリックな手法は基本的にモデルを想定し、そこからトップダウンでパラメータを推定するが、ノンパラメトリックな手法はデータからボトムアップでモデルを生成する。

ノンパラメトリックな推定

カーネル密度推定、k近傍法、局所回帰（LOESS）、平滑化スプライン、決定木、ランダムフォレストなどのノンパラメトリックな推定方法があるが、これらは基本的にボトムアップでデータからモデルを生成する方法だ。例えば、従来の回帰分析などのカーブフィッティングは何らかのモデルを想定し、最尤法によりパラメータを最適化させたが、カーネル密度推定、k近傍法、局所回帰（LOESS）、平滑化スプラインなどといった方法は、データポイントの近くのデータだけをローカルに繋ぎ、それをさらにグローバルに繋げていくという方法により、最初にモデルを想定（仮定）することなくモデルを生成する。例えば、k近傍法の場合、k=3などと設定して、データポイントから3つまでの近しいデータと平均を取る。これを繋げていくことによってグローバルなモデルができることとなる。他の手法も数学的なオペレーションは異なるものの基本的な考え方は同じだ。これらは当然機械学習（ML）でよく使われるものだ。

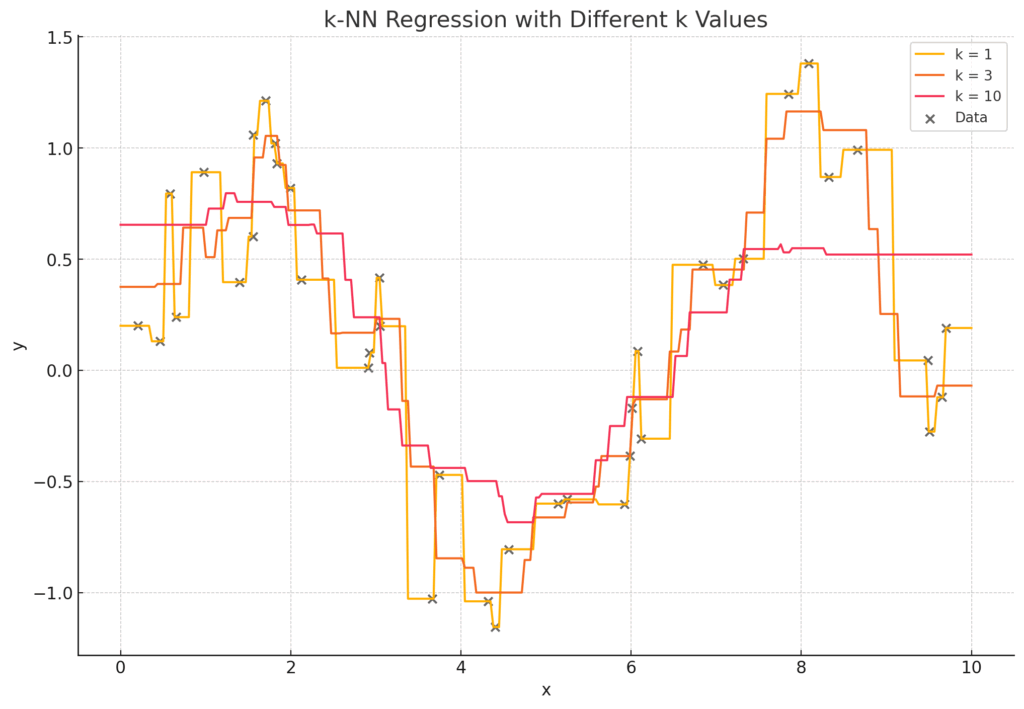
しかし、一度立ち止まって考えてみると、k近傍法の場合、なぜk=3なのか、という疑問が浮かんでくる。そしてK=データ数（N）と設定してやればデータと完全一致するモデルを構築することができるということになる。これは従来型の回帰分析などのカーブフィッティングで多項式の次数をデータNに対してN-1と設定する（およびパラメータを調整する）ような話で、そのようなことをすれば、当然データと完全一致するモデルを構築することができる。しかしこれは当然ながらオーバーフィッティング（過学習）であり、手元に存在するデータを丸暗記したにすぎず、新しいデータを予測することはできない。このような際に従来型のパラメトリックなカーブフィッティングではAICなどを用いたが、ノンパラメトリックな手法の場合、交差検証（Cross Validation）を用いる。交差検証はデータをトレーニングセットとテストセットに分割して、トレーニングセットで学習したモデルがテストセットを予測することができるかという形でモデルを検証する。ちなみにTake-One-Out-Cross-Validationと呼ばれる交差検証は特定条件下でAICと等値となる。それによりこのkの数を調節する。このkのようなものはハイパーパラメータと呼ばれ、カーネル密度推定、局所回帰（LOESS）、平滑化スプラインなども基本的には同じような考え方であり、交差検証によりハイパーパラメータを調整してモデルを生成する。

決定木はデータ空間を二分割に分けて、何らかのルールに従い、右に行くのか左に行くのかを決める。それにより分類であったり回帰であったりを可能にする。もちろんこのルールも交差検証によって調整される。ランダム・フォレストは決定木の集合体（アンサンブルと呼ばれる）を用いて分類であったり回帰であったりをおこなう（故にフォレスト）。この際、ブートストラップ法（リサンプリング手法）によりデータから複数のリサンプリングを行い、独立した木をたくさん作る。会期の場合それらを平均し、分類の場合それらの多数派を取る。こうすることによってより精度の高い予測ができることが知られている。

ノンパラメトリックな仮説検証

ウィルコクソン検定

ノンパラメトリックな仮説検証にも頻度主義的なものとベイズ統計的ものがある。頻度主義的なものはp値を用いる。有名なものがウィルコクソン検定と呼ばれるもので、これはフランク・ウィルコクソンが1945年に提案したもので、いまだベイズ統計がマイナーな時期であり、フィッシャー（頻度主義統計）の影響が色濃く見られる。

今、以下のような二つのデータがありこれらが同じ確率分布から来たものかどうなのかを検証したいとしよう。

Group A: [75, 80, 85, 70, 90]

Group B: [65, 60, 70, 55, 75]

まずはデータを統合する。

全データ=[75, 80, 85, 70, 90, 65, 60, 70, 55, 75]

次に順位を割り当てる（同順位は平均する）。

値	順位
55	1
60	2
65	3
70	4.5
70	4.5
75	6.5
75	6.5
80	8
85	9
90	10

次にGroup Aの順位の合計を求める。Group Aの対応する順位は: [6.5, 8, 9, 4.5, 10]

その合計: RA = 6.5 + 8 + 9 + 4.5 + 10 = 38

次に期待値と分散を求める。順位和の期待値（平均）は

\[\mu_R = \frac{n_1(n_1 + n_2 + 1)}{2} = \frac{5 \cdot (5 + 5 + 1)}{2} = \frac{5 \cdot 11}{2} = 27.5\]

であり、分散は

\[\sigma_R^2 = \frac{n_1 n_2 (n_1 + n_2 + 1)}{12} = \frac{5 \cdot 5 \cdot 11}{12} = 22.92\]

であり、ここからZスコア

\[Z = \frac{R_A – \mu_R}{\sqrt{\sigma_R^2}} = \frac{38 – 27.5}{\sqrt{22.92}} \approx \frac{10.5}{4.79} \approx 2.19\]

が求められる。

\[p \approx 0.028 < 0.05\]

なので帰無仮説は棄却される（Zを求めればp値はZテーブルと呼ばれる表を見れば得られる）。

ベイズ的仮説検定

もう少しベイズ的仮説検証だと以下のようになる。まずGroup Aからサイズ5のリプレイスありの復元抽出でサンプルを1つ取得し、Group Bでも同様に、サイズ5の復元抽出を行い、それらの平均の差を計算する。そしてこの処理を 10,000回繰り返して、平均差の分布を構築する。こうすることにより

\[\mu_A – \mu_B \text{ に対するブートストラップ事後分布}\]

を得ることができる。今回のケースでは10,000 回のブートストラップサンプリングのうち、約 9,997 回が

\[\mu_A > \mu_B\]

となった。つまり

\[\text{事後確率}(\mu_A > \mu_B) = \frac{9997}{10000} = 0.9997\]

であり、Group Aの平均がGroup Bよりも大きいという事後確率は 99.97%ということになる。これはベイズファクターのように比率を用いているので、（ベイズファクターではないが）ベイズ的であると言える。

ちなみにここではブートストラップ手法を用いているので、厳密にいうと尤度原理に反している。ここでブートストラップ手法を用いた理由は計算負荷を下げるためだ。やはり頻度主義よりベイズ統計の方が良いとは思うが、ベイズ統計は計算負荷が高いのが難点だ。