回帰分析とは最も単純には二つの変数間の相関関係を調べる統計学の分析手法である。二つの変数は独立変数と従属変数に別れ、機械学習では独立変数は特徴量、従属変数はターゲットと呼ばれる。従属変数(ターゲット)が私たちが説明したい変数(被説明項)であり、独立変数(特徴量)は従属変数を説明する変数(説明項)である。回帰分析はデカルト座標系(X-Y座標系)で図示され、独立変数はX軸、従属変数はY軸にプロットされる。例えば、子どもの身長をYとして親の身長をXとして、親子の身長のペアをデカルト座標系にプロットして、それらの点(データ)を一つの直線で繋ぐと親の身長が高くなるにつれ、子どもの身長が「どの程度」高くなるのかという相関関係を求めることができる。つまり、例えば、「親の身長が1cm高くなれば、平均して子どもの身長は2cm高くなる」というような説明ができることになる(実際には回帰分析を発見したゴルトンが回帰分析を回帰分析と名付けたように、身長は平均へ回帰する(regress to the mean)。そうでなければ、将来的にとても大きな人ととても小さな人ができることになってしまう。これが回帰分析の名前の由来であるが、現在の回帰分析は別に平均への回帰がないものも分析する)。もちろん(よほど例外的な事象でない限り)通常、点(データ)は一直線上にないので、点(データ)から直線への距離(下記図の点線)が最小(least)になるような直線を描く(下記図)。この際、幾つかの点(データ)は直線の上(プラス)にあり、幾つかは下(マイナス)にあり、プラスとマイナスを足し合わせると記号が相殺してしまうので、そうならないように距離を二乗(square)する。この方法は最小二乗法(least square method)と呼ばれる。
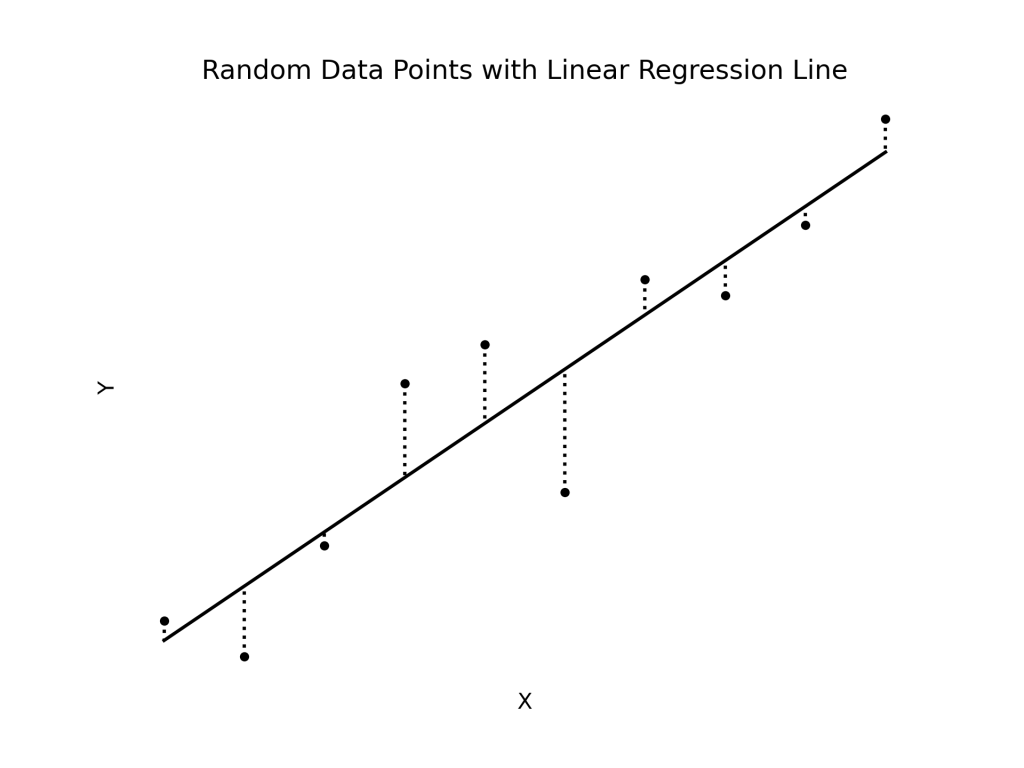
回帰分析は基本的にパラメータの最適化である。パラメータは係数であり、「親の身長(X)が1cm高くなれば、平均して子どもの身長(Y)は2cm高くなる」といった場合、回帰線は
\(Y=2X+e\)
\(子どもの身長=2×親の身長+誤差項\)
と表され、ここで2がパラメータ(係数)に当たる(ここでは切片を落としている)。eの誤差項(error)は直線と点(データ)の距離(上記図の点線)である。パラメータ(係数)は直線の傾きであり、この傾きをXとYというデータから求めることが回帰分析である。これをビッグデータに基づき機械にやらせるのが機械学習(の一種)である。まとめると
\(従属変数=パラメータ×独立変数+誤差項\) (統計学の場合)
\(ターゲット=パラメータ×特徴量+誤差項\) (機械学習の場合)
ということになる。数学の場合だと
\(Y=aX+b\)
という式はaとbは定数であり(aが傾き、bがY軸と交わる切片)、XとYは変数であるが、統計学および機械学習の場合はデータとして収集され既に手元に存在するXとYから
\(Y=aX+b+e\)
という式を使って、aとbおよびeというパラメータを推測するというように操作が逆になる。
話は逸れるが、なぜX-Y座標系をデカルト座標系と言うかというと、哲学者であり数学者だったルネ・デカルトは朝起きが苦手で、朝はベッドの上で読書や書き物をしていたらしいのだが、ある日、壁にハエがとまっているのを見て、壁をX-Y座標系で表現したらハエの正確な位置を記述できると考えた、というエピソードに由来する。同時代人だった数学者ピエール・ド・フェルマーらも同じようなことは考えていたようである。因みにデカルトはスエーデンの女王に家庭教師を頼まれ、女王の頭が一番冴えている朝5時くらいに授業をしてほしいと言われ、早起きして、それが原因で亡くなってしまった。
このように独立変数と従属変数の二変数を最小二乗法による直線で繋ぐというのが回帰分析の基本形であるが、もちろんこれは基本中の基本であり、実際には独立変数の数は一つでない場合が多いし、独立変数と従属変数を繋ぐ線も必ずしも直線とは限らない。最小二乗法も標準的な前提の元で、フィッシャーの考えだした最尤推定に変換することができる(モデルが線形であること。直線と点(データ)の間の誤差が標準分布に従い、独立である(自己相関がない)こと。そして誤差の分散が同一であること)。最小二乗法は計算が楽であるので、計算機(コンピュータ)が存在しなかった時代には使いやすかった。
独立変数は当然増える。例えば、子どもの身長を説明するのは親の身長だけでなくて、栄養などといったものも考えられる。何が被説明項である従属変数(ターゲット)をうまく説明できるのかを考えることはおそらくは回帰分析のモデリングの中で最も重要であり、機械学習では特徴量エンジニアリングと呼ばれる。ここには主成分分析(principal component analysis, PCA)など様々な手法がある。また回帰線は直線でない場合も考えられる。直線の場合、独立変数と従属変数の関係性は一定であるが、そうでない場合も考えられる。こういった場合、情報量基準や交差検証などが用いられる。
