有意検定

フィッシャーの統計学は1920年代にロサムステッド研究所で始まる。フィッシャーはミュリエル・ブリストルという女性に紅茶を出した。フィッシャーがミルクより先に紅茶をカップに注いだところ、彼女はフィッシャーに抗議し、ミルクを先に入れるか紅茶を先に入れるかで味が違い、彼女は味の違いを分別することができると言った。そこでフィッシャーは彼女が本当に味の違いを分別することができるのか確かめるために古典的統計実験を作り上げた。

今、ミルクを先に入れた紅茶とミルクを後に入れた紅茶が6組あるとしよう（フィッシャーのオリジナルの実験では4組）。そして実は彼女が全く違いを分からないと仮説を立てよう。これは帰無仮説と呼ばれる。彼女に6組の紅茶を飲ませて、違いを当てさせるという実験を行い、

（正解、正解、正解、正解、正解、間違い）

という結果が出たとする。全てのペアは1/2の確率でミルクを先に入れた紅茶とミルクを後に入れた紅茶であるので、この結果が出るのは1/2の6乗=1/64である。ここで考えられる可能性は二つある。

a) 帰無仮説が正しいのだが、とても確率の小さいことが起こった（彼女は本当は違いがわからないのに偶然5回も当ててしまった）

b) 帰無仮説は間違いで、ミュリエル・ブリストルは本当に違いがわかる

ここで、「とても確率の小さいこと」というのは1/64という確率で起こった本当はわかっていないのに偶然5回も当ててしまったことである。しかし1/64という確率はあまりにも小さいので、帰無仮説は間違いで、ミュリエル・ブリストルは本当に違いがわかると考えると、この実験結果は1/64の確率で有意であるということができる。この1/64というのがこの場合の有意水準（α）である。今日では有意水準には5%などが使われる。

しかしここで独立同分布（IID）という前提を思い起こしてみるとこの考え方は間違っているということになる。IIDとは各事象は独立であり、各々の事象は同じ確率分布（今回は1/2）に従っているという前提である。この前提を受け入れるならば、

（正解、正解、正解、正解、正解、間違い）

（正解、正解、正解、正解、間違い、正解）

……

などどのような結果（順列）が出てもそれらの確率は全て同じ（1/2の6乗=1/64）ということになる（5回続けて正解なのだから、そろそろ間違いが来るだろう、といったようなIIDを疑ってしまう考え方はギャンブラーの誤謬と呼ばれる）。フィッシャーはこのような事態を避けるために順列ではなく組み合わせを使うことにした。順列の場合、順序が関係あるが、組み合わせの場合は順序は関係ない。例えば、上記の

（正解、正解、正解、正解、正解、間違い）

（正解、正解、正解、正解、間違い、正解）

という二つの結果は順列では異なるものと考えられるが、組み合わせでは同じと考える。組み合わせで考えるならば、6つの可能性があるということになり、6×1/64=6/64=.094となり、棄却水準α=5%で有意ではない、つまり上記のa) 帰無仮説が正しく、とても確率の小さいことが起こった（彼女は本当は違いがわからないのに偶然5回も当ててしまった）ということになる。

しかしこれもまだ問題を含んでいる。純粋な当てずっぽうで最も確率が高いのはなんだろうか、と考えた時に当然それは半分が正解で半分が間違い、というものである。IIDに従うコイン投げを考えてみればわかりやすいが、公正なコインを100回投げた時に、最も確率が高い出方は50回表、50回裏だろう（下記の点推定）。つまり.05ということになる。そしてこれ以外の確率はより小さいということになる。

もし純粋な当てずっぽうの確率が最大（.05）で、それ以外がそれよりも低いとすると、どのような確率も棄却水準5%で有意ということになってしまう。これを避けるためにフィッシャーは6回のうち間違い1回が有意であるならば、それよりも極端な場合である6回のうち間違い0回も有意であるに違いないと考えた。つまり実際に観察された結果およびそれよりも可能性が低い場合を計算に含めるということになる。p値の誕生である。p値は得られたデータの尤度およびそれより極端な状況の尤度を足し合わせたものである。つまりフィッシャーの仮説検証（有意検定）は尤度に基づいている。因みに、実際にフィッシャーが実験を行ったところ、ミュリエル・ブリストルは全て正確に言い当てたようだ。

ストッピング・ルールの問題

紅茶と有意検定の話はフィッシャーが1935年に出版した『実験のデザイン（The Design of Experiments）』の第二章に出てくる。どのようにして仮説を検証するための実験を行うかをフィッシャーは論じたのだ。しかし有意検定の一つの問題はまさに実験デザインに関わる問題である（この指摘はハロルド・ジェフリーズ、J.B.S. ホールデン、デニス・リンドリーあたりからきている）。いつどのように実験を終えるのかというルールのことをストッピング・ルールと呼ぶ。問題はどのようなストッピング・ルールを採用するかで有意か有意でないかの結果が180度変わってきてしまう。

I・J・グッドがベイズファクターと名付けたベイズ的手法を用いるとストッピング・ルールの問題は回避することができる。この辺りの話は『本当の声を求めて：野蛮な常識を疑え』に書いている。もちろんこれはベイズファクターが万能であるということではない。万能な道具などない。要は道具を状況に応じて使い分ける能力が必要なのだ。

（点）推定

因みにこのような正解か間違いか、表か裏か、といったような分布は二項分布と呼ばれるが、「コインは公正である（表=裏=½）」とか「ミュリエル・ブリストルは違いがわからない（彼女の選択はランダムである）（正解=間違い=½）」などと仮説を設定した時の尤度P(O|H)を最大化させることは最大値（もしくは最小値）を探すことに等しい。このような単純な場合は図をみれば一目瞭然なのだが、理論的には分布図に接する線の傾きを0にする作業である（下記図）。曲線に対する接線は曲線の微分を取れば良いので、微分＝0になるポイントを探すことになる。これがフィッシャーの考えた（点）推定であり、それは尤度P(O|H)を最大化させる最大尤度（一点）を求めることに等しい（このような単純な場合には、微分が使えるが、曲線が複雑な場合には局所的な最大値に捕まってしまうことがあるため、勾配法などといった方法を用いる。これは微分の逆操作である積分が難しい時にモンテカルロ手法などを用いることと似ている）。

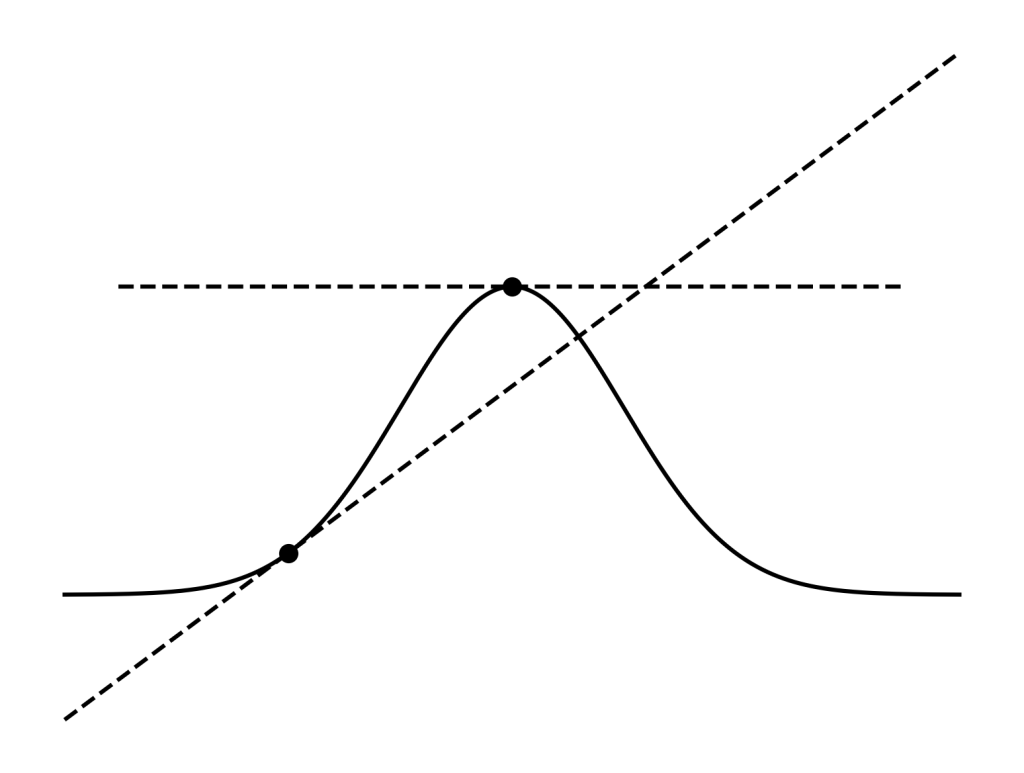
図を見れば、どこで接線の傾きが0になるかわかる。

今n回コインを投げてk回表が出る（もしくはn回紅茶のテイスティングをしてk回正解が出る）確率は

\(\binom{n}{k} p^k (1-p)^{n-k}\)

と定義できる。対数（log）を取ると掛け算は足し算に、〜乗の部分は係数として前に出るので、

\(\log \binom{n}{k} + k \log p + (n-k) \log (1-p)\)

が得られる。これを微分する（微分についても時間があれば簡単な解説を書きたい）。\(\binom{n}{k} \)は\(\frac{n!}{k!(n-k)!} \)なので定数であり、定数は微分すると消えるので最終的に、

\( \frac{d}{dp} \left[ k \log p + (n-k) \log (1-p) \right]\)

となる。対数を微分すると、何分の1という形になるので、

\(\frac{k}{p} – \frac{n-k}{1-p} \cdot (-1)\)

が得られる（最後に\(-1\)が出現するのは、連鎖律（chain rule）と呼ばれるものの結果で、\(f(x)\)と\(g(x)\)をそれぞれ関数として、\(f(x)\)の中に\(g(x)\)が入っている（この入っているというのをnestedと言う）。\(f(g(x))\)のような関数のことを合成関数（composite function）と呼ぶが、合成関数を微分するときには連鎖率が適用される。この場合\(f(x)\)が\(log\)であり\(g(x)\)が\(1-p\)なので、\( log(1-p)\)の形になっている。こういった場合、まず\(f(x)\)を微分して、次に\(g(x)\)を微分してそれらを掛け合わせる。\(log(1-p)\)の微分は\(\frac{1}{1-p}\)で、\( 1-p\)の微分は\(-1\)である）。これを解くと

\(\frac{k}{p} + \frac{n-k}{1-p}\)

がえられ、これを0に設定して解くと、

\(\frac{k}{p} + \frac{n-k}{1-p} = 0\)

\(\frac{k}{p} = -\frac{n-k}{1-p}\)

\(k(1-p) = -p(n-k)\)

\(k – kp = -pn + pk\)

\(k = pn\)

\(p = \frac{k}{n}\)

が得られる。これは上記の図の頂点の部分、接線の傾きが0のところである。当然、「コインは公正である（表=裏=½）」とか「ミュリエル・ブリストルは違いがわからない（彼女の選択はランダムである）（正解=間違い=½）」などと仮説を設定した時の最大尤度は1/2となる。フィッシャーは尤度に基づいて、仮説検定（有意検定）と（点）推定という区別を作ったが、これらは両方尤度に基づいている。

後年のロナルド・フィッシャー（右端）